構文木にIdを振りたい。

構文木に情報を追加したいときにFix使うとちょっと楽だよっていう話。
例えば

data Term = Var String | Lam String Term | App Term Term

みたいなデータの各ノードにIdを振りたいとする。
ナイーブにやると

data ITerm = IVar Int String | ILam Int String ITerm | IApp Int ITerm ITerm

こんな感じになるだろうか。
コンストラクタの名前が変わって冗長だ。

これに対してFixを使うとこうなる。

newtype Fix f = In (f (Fix f))

data TermF a = Var String | Lam String a | App a a
newtype ITermF a = ITermF (Int, TermF a) 
newtype Term = Term (Fix TermF)
newtype ITerm = ITerm (Fix ITermF)

これなら他に型情報とかを追加したくなってもnewtypeで簡単に追加できる。
Idを振るサンプルは以下のとおり。

cata :: Functor f => (f a -> a) -> Fix f -> a
cata f (In t) = f (fmap (cata f) t)

incr :: State Int Int
incr = do
    i <- get
    put $! i + 1
    return i

assignId :: Term -> State Int ITerm
assignId (Term _t) = ITerm <$> cata f _t where
    f (Var s) = c $ pure $ Var s
    f (App t1 t2) = c $ App <$> t1 <*> t2
    f (Lam x t) = c $ Lam x <$> t
    c t = In . ITermF <$> ((,) <$> incr <*> t)

newtype同士のキャストがだいぶ煩雑になってしまうのが玉に瑕だ。

詳細なコードは以下のgistにある。
gist0b9f189fd5cf0550903e

let式の構文解析

導入

以下のBNF*1は足し算とlet式からなる式を表す。

<digit> ::= [0-9]
<alphabet> ::= [a-zA-Z]
<int> ::= <digit> | <digit><int>
<id>  ::= <alphabet> | <id>
<expr> ::= <int> 
        |  <id> 
        |  '(' <expr> ')' 
        |  "let" <id> '=' <expr> "in" <expr>
        |  <expr> '+' <expr>

さて、この文法には２つの曖昧性がある。一つは足し算の結合性、もう一つはlet式と足し算の優先順位の曖昧性だ。

1 + 2 + 3 => 
    (+ (+ 1 2) 3) 
  | (+ 1 (+ 2 3))
let x = 1 in 2 + 3 => 
    (let (x 1) (+ 2 3)) 
  | (+ (let (x 1) 2) 3)

ここでは曖昧性を解決するために足し算は左結合とし、足し算がlet式に優先するとしたい。

そのような文法はPEG*2で以下のように表現できる。

INT <- [0-9]+
ID  <- [a-zA-Z]+
P   <- INT / ID / '(' E ')' / "let" ID '=' E "in" E
E   <- E ('+' P)*

今回の記事ではこのような文法を曖昧性のない文脈自由文法で定義してみる。

最初の試み

自然に考えられる文法として以下のようなものがある。

<prim> ::= <int> | <id> | '(' <expr> ')' 
<term> ::= <prim> | <term> '+' <prim>
<expr> ::= <term> | "let" <id> '=' <expr> "in" <expr>

この文法は上の二つの例を正しくパーズする。

1 + 2 + 3 => (+ (+ 1 2) 3) 
let x = 1 in 2 + 3 => (let (x 1) (+ 2 3))

しかし、この文法は期待する言語を表現していない。例えば次のような式をパーズできない。

1 + let x = 1 in x => Error!

次の試み

上の例からprimがlet式を含まなければならないということがわかった。
しかしprim '+' exprとなっている場合はprimがlet式を含んでいてはならない。
つまり、足し算の第２オペランドにlet式が出現できるかどうかを区別する必要が有る。

<atom> ::= <int> | <id> | '(' <expr> ')'
<prim> ::= <atom> | "let" <id> '=' <expr> "in" <expr>
<term> ::= <atom> | <term> '+' <atom>
<expr> ::= <prim> | <term> '+' <prim>

この文法は期待する言語を表現する。

1 + let x = 1 in x => (+ 1 (let (x 1) x))
1 + let x = 1 in 1 + 2 => (+ 1 (let (x 1) (+ 1 2)))
1 + (let x = 1 in x) + 3 => (+ (+ 1 (let (x 1) x)) 3)

yaccによる動作確認

この文法に曖昧性がないことを確かめるためにyaccに書き下す。

Parsing

yaccがconflictを出さなかったのでこの文法は曖昧でない。

ちなみに動作例。

$ ocamlbuild main.native
$ ./main.native
1 + let x = 1 in x + x
Plus(1, Let(x, 1, Plus(x, x)))
1 + 2 + 3
Plus(Plus(1, 2), 3)
1 + (2 + 3)
Plus(1, Plus(2, 3))
(let x = 1 in let y = 2 in x + y) + 3
Plus(Let(x, 1, Let(y, 2, Plus(x, y))), 3)

yaccのPrecedenceについて

上のようなパーサはyaccのPrecedenceを適切に設定することによっても得ることができる。

gist114a58bce2ab6af47926

このPrecedenceがどう働くかは
http://dinosaur.compilertools.net/yacc/
に記述がある。

The precedences and associativities are used by Yacc to resolve parsing conflicts; they give rise to disambiguating rules. Formally, the rules work as follows:

1. The precedences and associativities are recorded for those tokens and literals that have them.

2. A precedence and associativity is associated with each grammar rule; it is the precedence and associativity of the last token or literal in the body of the rule. If the %prec construction is used, it overrides this default. Some grammar rules may have no precedence and associativity associated with them.

3. When there is a reduce/reduce conflict, or there is a shift/reduce conflict and either the input symbol or the grammar rule has no precedence and associativity, then the two disambiguating rules given at the beginning of the section are used, and the conflicts are reported.

4. If there is a shift/reduce conflict, and both the grammar rule and the input character have precedence and associativity associated with them, then the conflict is resolved in favor of the action (shift or reduce) associated with the higher precedence. If the precedences are the same, then the associativity is used; left associative implies reduce, right associative implies shift, and nonassociating implies error.

要約すると、各ruleの一番最後に現れるtokenのprecedenceをそのruleのprecedenceとし、パーサを構成する過程でconflictが起こったところでprecedenceの高いruleを選択するという仕組みのようだ。
どうにもad-hocに思えてならないのだが、上手くいく裏付けが何かあるのだろうか。

*1:バッカス・ナウア記法 - Wikipedia

*2:Parsing Expression Grammar - Wikipedia

Haskell組み込みDSLでSVGを書く

概要

プログラムで画像を作りたい時に便利そうなのでメモ。

diagrams-svg: SVG backend for diagrams drawing EDSL. | Hackage
これはHaskellでVector画像を描くライブラリである、diagramsライブラリのSVG出力ライブラリとなっている。
diagrams-lib: Embedded domain-specific language for declarative graphics | Hackage

一応githubにチュートリアルっぽいものがあるのだが、
それは型エラーでコンパイルできなかった。

今回は使い方を確認するために有名なフラクタル図形を書いてみた。
シェルピンスキーのギャスケット - Wikipedia

コード


gistb4b778a917a59693a7a7

コンパイルと実行

$ ghc --make Sierpinski.hs
$ ./Sierpinski -o image.svg 10 5

コマンドライン引数で渡した10と5が図形のパラメータとしてコード中で使用することができて便利だ。

出力される画像はこんな感じになる。
f:id:autotaker:20150226140328p:plain

簡単なコード解説

main :: IO ()
main = mainWith d where
    d c k = pad 1.1 $ sierpinski c k # lcA transparent # fc (sRGB 0.3 0.3 0.3)

mainWithという関数がdの型から適切にコマンドライン引数をパーズしてdに渡してくれる。
関数dはパラメータcとkをつけとって図形を返す。
ここでcとkはそれぞれ最小の三角形のサイズと再帰の深さを表すパラメータで、
ではsierpinski c kという図形の線の色(lcA)や塗りつぶしの色(fc)を指定して、
1割の余白(pad)を付与する。

sierpinski :: Double -> Int -> Diagram B R2
sierpinski c 0 = triangle c 
sierpinski c k = 
    let d' = sierpinski c (k-1)
        l  = c * 2^(k-1) 
        z  = sqrt 3 / 2 * l / 3 
        ps = [(0,z*2),(-l/2,-z),(l/2,-z)] in
    position $ map (\p -> (p2 p,d')) ps

Diagram B R2という型においてBはバックエンドの型（ここではSVG）、R2は２次元画像を意味する。*1
再帰の深さがリミットに達した場合は一辺の長さがcの正三角形(triangle c)を返し、
そうでない場合は、siperpinski図形を生成し（sierpinski c (k-1)）、それを３箇所に並べた(position)ものが
siperpinski図形となる。

このようにして図形を代数的にかけるのでとてもイイ感じのライブラリだ。

*1:ちなみにDiagram B R2はMonoidのインスタンスになっているので、複数の図形を書きたい場合はd1 <> d2みたいに すればよい。

ELF解析のはじめ

linuxの実行バイナリであるELFファイルの解析の仕方のメモ

IBMのスライドを参考にした。
http://www-06.ibm.com/jp/linux/tech/doc/attachments/002cb129_elf_v1_0.pdf

サンプルELFの作成

まず、サンプルとなるプログラムを用意する。

// func.c
#include <stdio.h>

int global_num = 0xaa00;

int func1( int i )
{
  return global_num + i;
}

int func2( int i )
{
  return global_num + i + i;
}

//main.c
#include<stdio.h>

extern int global_num;
extern int func1( int i );
extern int func2( int i );

int main( void )
{
  printf( "global_num = %04x\n", global_num );
  printf( "func1( 0x11 ) = %04x\n", func1( 0x11 ) );
  printf( "func2( 0x22 ) = %04x\n", func2( 0x22 ) );
}

gccでコンパイルして実行バイナリを作る。

$ gcc -O0 -g -c -o func.o func.c
$ gcc -O0 -g -c -o main.o main.c
$ gcc -o main func.o main.o

解析に入る前に

まず、objdumpを使って逆アセンブルとデータを書き出しておく。

$ objdump -M intel -S main > main.txt
$ objdump -s main > main.data

解析

.textセクションの最初から実行されるということなのでそこを見てみる。

Disassembly of section .text:

08048320 <_start>:
 8048320:	31 ed                	xor    ebp,ebp
 8048322:	5e                   	pop    esi
 8048323:	89 e1                	mov    ecx,esp
 8048325:	83 e4 f0             	and    esp,0xfffffff0
 8048328:	50                   	push   eax
 8048329:	54                   	push   esp
 804832a:	52                   	push   edx
 804832b:	68 10 85 04 08       	push   0x8048510
 8048330:	68 a0 84 04 08       	push   0x80484a0
 8048335:	51                   	push   ecx
 8048336:	56                   	push   esi
 8048337:	68 42 84 04 08       	push   0x8048442
 804833c:	e8 cf ff ff ff       	call   8048310 <__libc_start_main@plt>
 8048341:	f4                   	hlt    
 8048342:	66 90                	xchg   ax,ax
 8048344:	66 90                	xchg   ax,ax
 8048346:	66 90                	xchg   ax,ax
 8048348:	66 90                	xchg   ax,ax
 804834a:	66 90                	xchg   ax,ax
 804834c:	66 90                	xchg   ax,ax
 804834e:	66 90                	xchg   ax,ax

0x8048510, 0x80484a0, 0x8048442というのは
それぞれ__libc_csu_fini, __libc_csu_init, mainの関数ポインタのようだ。

それらを適当にスタックに積んだ後で
__libc_start_main@pltという関数を呼び出している。
__libc_start_main@pltというのはどうなっているかというと、

08048310 <__libc_start_main@plt>:
 8048310:	ff 25 14 a0 04 08    	jmp    DWORD PTR ds:0x804a014
 8048316:	68 10 00 00 00       	push   0x10
 804831b:	e9 c0 ff ff ff       	jmp    80482e0 <_init+0x2c>

0x804a014のポインタ先に間接ジャンプしているらしい。
よくわからないのでIBMのスライドを見てみると、共有ライブラリの関数を呼ぶ場合は
実行時に関数ポインタが書き込まれるとのことだ。

gdbで実行してみる。

$ gdb main
(gdb) b *0x8048510
(gdb) b *0x80484a0
(gdb) b *0x8048442
(gdb) run
Breakpoint 2, 0x080484a0 in __libc_csu_init ()
(gdb) info stack
#0  0x080484a0 in __libc_csu_init ()
#1  0xb7e2d89a in __libc_start_main (main=0x8048442 <main>, argc=1,
      ubp_av=0xbfffebd4, init=0x80484a0, <__libc_csu_init>,
      fini=0x8048510 <__libc_csu_fini>, rtld_fini=0xb7fed5f0 <_dl_fini>,
      stack_end=0xbfffebcc) at libc-start.c:219
#2  0x08048341 in _start ()

__libc_csu_initが呼び出された。この関数が何をやっているのかはよくわからないので
次に進むとmainが呼び出されている。

main部分は簡単に読むことができた。

KleisliでもArrowしたい。

Haskellの話。

Control.Arrow
というライブラリがあるのだが、自分に取っては
first, second, (***),(&&&)くらいを使うくらいのユーティリティライブラリでしかなかった。

class Category cat where
    id :: cat a a
    (.) :: cat b c -> cat a b -> cat a c

(>>>) :: Category cat => cat a b -> cat b c -> cat a c
a >>> b = b . a

class Category a => Arrow a where
    arr :: (b -> c) -> a b c
    first :: a b c -> a (b,d) (c,d)
    second :: a b c -> a (d,b) (d,c)
    (***) :: a b c -> a b' c' -> a (b,b') (c,c')
    (&&&) :: a b c -> a b c' -> a b (c,c')

(>>>)は射の合成、first,secondはそれぞれペアの第１要素、第２要素のみを変更する射、
(***)は射の積、(&&&)は一つのソースを二つに分割する射となっている。

最近モナドでfirst, secondを使いたくなるときがあったのでメモ。
具体的には次のようなコードだ

splitBy :: [a] -> Int -> [[a]]
splitBy [] _ = []
splitBy l  n = hd:splitBy tl n where
    (hd,tl) = splitAt n l

これはリーダーモナドを使って次のように書ける。

splitBy :: [a] -> Int -> [[a]]
splitBy [] = return []
splitBy l = do
    (hd,tl) <- flip splitAt l
    tl' <- splitBy tl
    return (hd:tl')

気持ち的には

splitBy l = fmap (uncurry (:)) $ flip splitBy l >>= second splitBy

のような感じで書きたいのだがsecondの型が合わない。
調べてみると

newtype Kleisli m a b = Kleisli { runKleisli :: a -> m b }
instance Monad m => Arrow (Kleisli m)

というinstanceを見つけたのでこれが使えそう。

splitBy :: [a] -> Int -> [[a]]
splitBy [] = return []
splitBy l = fmap (uncurry (:)) $ flip splitAt l >>= runKleisli (second (Kleisli splitBy))

これで型もあうのだが、>>=の右側がどうにも格好悪い。
他の例も考えてみてよい補助関数を見つけたいところだ。

ちょまどパズルの下界が8である証明

Intro

問題の発端はこのツイートから


何回で満点とれる？【ちょまど問題に挑む人々】 - Togetterまとめ

問題を形式化すると、

  • 入力として四択問題が10問与えられる。
  • 解答を提出すると正解数がフィードバッグされる。
  • 任意の入力に対して全問正解するまでに必要な最大質問数を最小化せよ。

決定木について

任意の入力パターン全問正解アルゴリズムは次のような決定木だと考えることができる。

  • 各節には提出する解答がラベルされている。
  • 各葉には正解がラベルされている。
  • 各節からのびる枝は解答に対するフィードバッグに応じてどの節に移るかが記されている。
  • 異なる入力が同じ葉にたどり着くことはない。
  • 葉に移る最後の質問は必ず全問正解しなければならない。

２択問題３問に対する決定木の例がこの図である。
f:id:autotaker:20140619125609p:plain
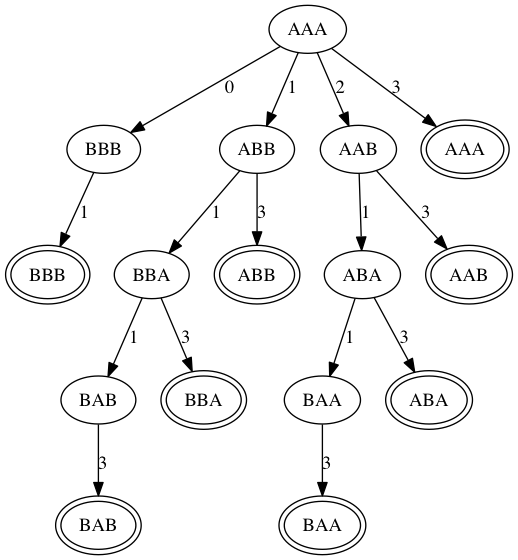
必要な最大質問数はこの決定木の高さに対応している。（この例では４回）

決定木の高さの見積もり

この木の高さを下から抑えることを考える。四択問題10問の場合、入力パターンは全部で{ 4^{10} = 1048576 }通りあり、葉の数も同数あり、各節から出る枝の数は高々11本なので、
高さ{h}の木に含まれる葉の数は高々{11^h}で、{11^h \geq 4^{10}}となる最小の
{h}は6なので少なくとも高さは6以上である。また最後の質問は全問正解しなければならないという制約があるので高さが7以上であることもすぐに分かる。

高さが8以上であることを示すにはもう少し踏み込んだ解析が必要である。
いままでの議論は各質問から11通りのフィードバッグがほぼ均等に分布するということを仮定している。しかし、例えば質問をして正解数が10となるのは一通りしかないので、各分岐には大きな偏りがあるはずだ。

まず最初の質問に対してどういう分布をするのかを考えよう。
最初の質問に対してのフィードバッグが{k}であるような入力のパターン数を{a_k}で表すことにすると、
{\displaystyle a_k = {}_{10}C_k 3^{10 - k}}
である。具体的に計算すると
{\displaystyle a_0 = 59049, \\ a_1 = 196830\\ a_2 = 295245\\ a_3 = 262440\\ a_4 = 153090\\ a_5 = 61236\\ a_6 = 17010\\ a_7 = 3240\\ a_8 = 405\\ a_9 = 30\\ a_{10} = 1}
従って、2問正解する分岐が一番多いことが分かる。
2問正解する分岐に対してその高さを見積もることを考えよう。
今{x}パターンの入力がその節に分岐すると仮定しよう。
11通りの分岐すべてに均等に分かれるとするとその節の子供のうち分岐するパターンが最も多いものは{\frac{x}{11}}通りである。しかし、先ほど見たように正解数10に分岐するパターンは高々一つなのでのこり10通りに均等に分かれると考えると{\frac{x-1}{10}}通りとなる。
同様に考えると分岐するパターンが最も多いものは少なくとも
{\max\{ \frac{x-a_{10} - \dots - a_{10-k+1} }{11-k} | 1 \leq k \leq 10 \}}
より大きいことが分かる。

この考えで解析していくと
深さiでのノードに分岐するパターン数の最大値は
1048576 -> 295245 -> 45760 -> 6012 -> 698 -> 75 -> 8 -> 1
というような下界を持つ。また、最後パターン数が１になったあとも全問正解するためにもう一回質問が必要になるので少なくとも8回の質問が必要である。

今回の議論もだいぶ粗い解析なのでもうちょっと深く解析すれば下界は改善できるのではないかとおもう。

10パズルを解いてみた。

数式の列挙問題を考えていてよくある例題として四つの数字と四則演算で１０を作るパズルを考えていた。

Wikipediaによるとこの問題のことを10パズルというらしい。
wikipedia:10パズル

本来やりたかったのは抽象構文木の列挙だったのだが、この問題は逆ポーランド記法を使うと簡単に書けるようだ。
【Ruby】【アルゴリズム】10パズルを解く。全ての数式を逆ポーランドで作る編 - せかいや

この10パズルの問題は大きく分けて３パターンある。一つは自然数の範囲内で解が存在するもの、二つ目は計算過程で有理数が出現してもよいという条件で解が存在するもの、もう一つは有理数を許しても解が存在しないものだ。

HaskellのListモナドを使えばきれいにこれらの制限をパラメータ化できそうなので実際に書いて解析してみた。


gist9562047

ideoneでの実行結果は以下の通り
http://ideone.com/Z9fOnO

1158,1199,1337,3478は自然数の範囲内では解が存在しないが、有理数の範囲では解が存在するという結果だった。それぞれの解は以下の通り
10 = \frac{8} {1 - \frac{1}{5}}
10 = 9 \times (\frac{1}{9} + 1)
10 = 3 \times (\frac{7}{3} + 1)
10 = 8 \times (3 - \frac{7}{4})
ちなみに自然数を整数に緩めた（引き算のときに負の数が現れてもよいとする）場合でも結果は変わらない。

電車の広告に難問として載っている物はどうせこれらのうちのいずれかなので覚えておくといいかも。