ちょまどパズルの下界が8である証明

Intro

問題の発端はこのツイートから


何回で満点とれる？【ちょまど問題に挑む人々】 - Togetterまとめ

問題を形式化すると、

  • 入力として四択問題が10問与えられる。
  • 解答を提出すると正解数がフィードバッグされる。
  • 任意の入力に対して全問正解するまでに必要な最大質問数を最小化せよ。

決定木について

任意の入力パターン全問正解アルゴリズムは次のような決定木だと考えることができる。

  • 各節には提出する解答がラベルされている。
  • 各葉には正解がラベルされている。
  • 各節からのびる枝は解答に対するフィードバッグに応じてどの節に移るかが記されている。
  • 異なる入力が同じ葉にたどり着くことはない。
  • 葉に移る最後の質問は必ず全問正解しなければならない。

２択問題３問に対する決定木の例がこの図である。
f:id:autotaker:20140619125609p:plain
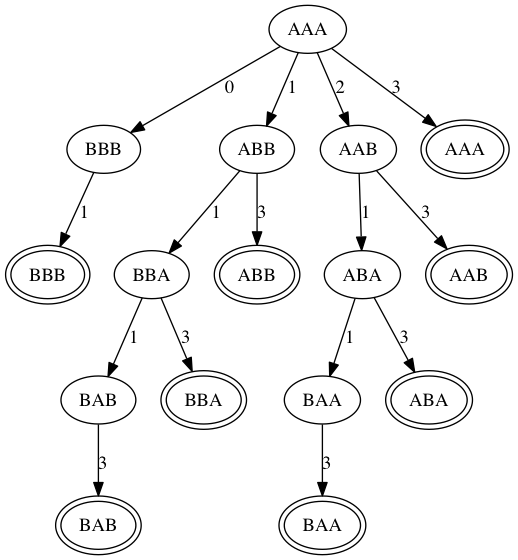
必要な最大質問数はこの決定木の高さに対応している。（この例では４回）

決定木の高さの見積もり

この木の高さを下から抑えることを考える。四択問題10問の場合、入力パターンは全部で{ 4^{10} = 1048576 }通りあり、葉の数も同数あり、各節から出る枝の数は高々11本なので、
高さ{h}の木に含まれる葉の数は高々{11^h}で、{11^h \geq 4^{10}}となる最小の
{h}は6なので少なくとも高さは6以上である。また最後の質問は全問正解しなければならないという制約があるので高さが7以上であることもすぐに分かる。

高さが8以上であることを示すにはもう少し踏み込んだ解析が必要である。
いままでの議論は各質問から11通りのフィードバッグがほぼ均等に分布するということを仮定している。しかし、例えば質問をして正解数が10となるのは一通りしかないので、各分岐には大きな偏りがあるはずだ。

まず最初の質問に対してどういう分布をするのかを考えよう。
最初の質問に対してのフィードバッグが{k}であるような入力のパターン数を{a_k}で表すことにすると、
{\displaystyle a_k = {}_{10}C_k 3^{10 - k}}
である。具体的に計算すると
{\displaystyle a_0 = 59049, \\ a_1 = 196830\\ a_2 = 295245\\ a_3 = 262440\\ a_4 = 153090\\ a_5 = 61236\\ a_6 = 17010\\ a_7 = 3240\\ a_8 = 405\\ a_9 = 30\\ a_{10} = 1}
従って、2問正解する分岐が一番多いことが分かる。
2問正解する分岐に対してその高さを見積もることを考えよう。
今{x}パターンの入力がその節に分岐すると仮定しよう。
11通りの分岐すべてに均等に分かれるとするとその節の子供のうち分岐するパターンが最も多いものは{\frac{x}{11}}通りである。しかし、先ほど見たように正解数10に分岐するパターンは高々一つなのでのこり10通りに均等に分かれると考えると{\frac{x-1}{10}}通りとなる。
同様に考えると分岐するパターンが最も多いものは少なくとも
{\max\{ \frac{x-a_{10} - \dots - a_{10-k+1} }{11-k} | 1 \leq k \leq 10 \}}
より大きいことが分かる。

この考えで解析していくと
深さiでのノードに分岐するパターン数の最大値は
1048576 -> 295245 -> 45760 -> 6012 -> 698 -> 75 -> 8 -> 1
というような下界を持つ。また、最後パターン数が１になったあとも全問正解するためにもう一回質問が必要になるので少なくとも8回の質問が必要である。

今回の議論もだいぶ粗い解析なのでもうちょっと深く解析すれば下界は改善できるのではないかとおもう。